But what do they mean?
What does it mean to ask how much grip the tire has?
How much is it soft or hard?
What does it mean to define soft a tire?.....they are terms better used to speak about the beef!
It would be the same if you comparing different engines say: it is more powerful or it is less powerful, it has more torque or less torque, without to know the torque and power concepts and without to associate the numerical values expressed in kW and Nm to those contents.
We clear up it giving the answers to some easy and intuitive questions.

What's the tire task? The answer is easy, the tire has to perform two tasks:
- allowing the transfer of drive force or brake force on the ground;
- generating the necessary lateral forces to maintain the motorcycle equilibrium in the curve or along a curvilinear path as for example those generated to avoid an obstacle, to carry out a line change or to run on a S shape curve.
Right now we try to understand how the lateral force is generated and how much it has to be when the motorcycle is running on steady turning condition with constant speed (stable condition) and which parameter the force depends from .

It is easy to understand that lateral force depends on normal vertical load applied on the wheel. High vertical load makes high lateral force. Understanding the dependence of lateral force upon the camber angle and tire sideslip (tire side-slip expressed by side-slip angle which will be defined later) is less intuitive.
The lateral force also depends on two more parameters which the bikers know very well: the tire pressure and the tire temperature in the work condition.
First we consider the camber angle effect. In vertical position the tire imprint is elliptical and symmetric; the tire imprint showed in figure 1 is painted with grey tones whose intensity is proportional to the pressure between the tire and the ground.

Figure 1. Vertical and tilted position tire imprints. The gray tone intensity is proportional to the pressure between the tire and the ground.

As you can observe in figure 1, when the wheel is tilted, the rubber particle that through the imprint doesn't follow the path that it would follow if there wasn't the contact between tire and ground. Because of there is contact with the ground the particle has to follow a different path, therefore the ground contact cause a deformation of tire carcass; this deformation generates a lateral force that increase when the camber angle increase.

Understanding better that phenomenon it is helpful to think about a shape-retaining tire, as if it was metallic; in that case the contact patch becomes like a point, there is not carcass deformation, hence the force due to the camber is null.

The camber force depends on shape and dimension of contact patch.

Contact patch depends on tire's geometric characteristics (rolling radius and cross section radius) and carcass lateral/radial stiffness.

Figure 2. Lateral and radial stiffness depend on pneumatic kind (front or rear), geometry, carcass constructive characteristics (radial, cross), pressure and normal load.

Right now we consider the lateral slip effect that is the side-slip angle

The side-slip angle is the angle between the forward direction and the central plane of the wheel. The contact patch is asymmetrical when the there is lateral slip. In the first part of contact patch the rubber particles tend to follow speed direction but, since the speed direction doesn't coincide to the wheel plane, the particles located inside contact patch are deformed with respect to tire carcass.
This is the contact patch part with adherence. When the deformation is al little more, the elastic recall forces due to the deformation of the rubber are greater then the adherence force so the particles start to slider. This is the contact patch part with slide. The integral of contact patch pressure give the lateral force due to the side-slip.

Figure 3. Side-slip force origin. The lateral pressure resultant is the lateral force due to the side-slip angle.

We saw the lateral force depends both roll angle and lateral slide of the tire; we expressed the tire lateral slip by means of side-slip angle.

Usually the lateral force is plotted against side-slip angle for various roll angles as represented in figure 4 for a race front tire.

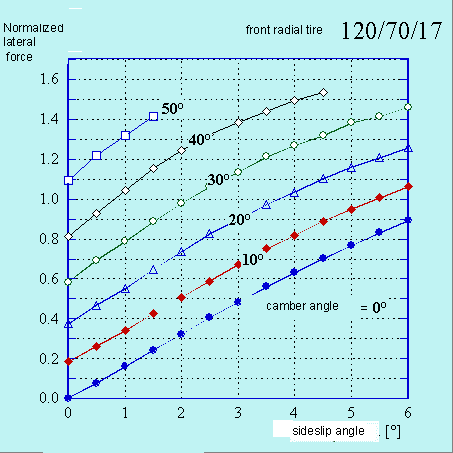
Figure 4. Lateral force against side-slip angle for various roll angles.

This kind of representation is used in the car field because the roll angle is very small and the tires make the required lateral forces only by the lateral slip. Otherwise the motorcycle tires work first by the roll and second by lateral slip, at least for the production of the lateral force. That's why for the motorcycle tires is better to represent the lateral force against roll angle for various side-slip angles as showed in the figure 5.

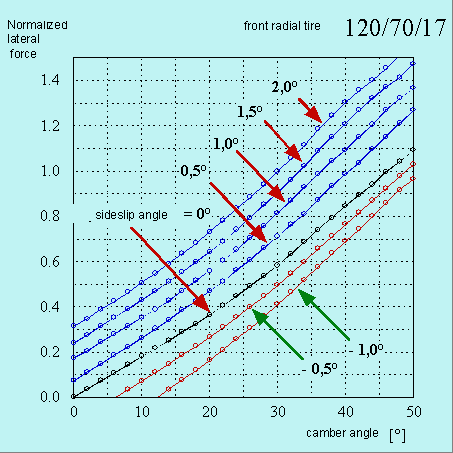
Figure 5. Lateral force against roll angle for various side-slip angles.

The lateral force can be expressed analytically by means of a linear function of roll angle and side-slip angle, thinking the force as sum of two independent components: the roll component and the side-slip component.

Force_lateral  = K_roll * j   + K _side-slip * l   

The K constants have a geometric meaning too; they represent the tangents of the curves respectively the normalized lateral force against roll angle with side-slip angle null and the lateral force against side-slip angle with roll angle null.

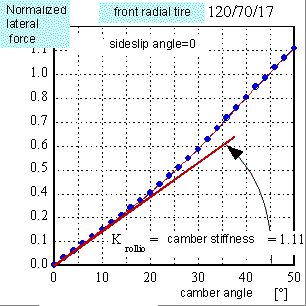
Figure 6.Roll and side-slip stiffness geometric meaning. Stiffness are expressed in 1/rad.

Force_lateral  =Load_vertical * tang j

Figure 7. Motorcycle equilibrium in the curve. R indicate the curvature radius of the curve, m the mass of the vehicle with driver and V the forward speed.

tang j= Force_lateral / Load_vertical = V²/ (g*R )

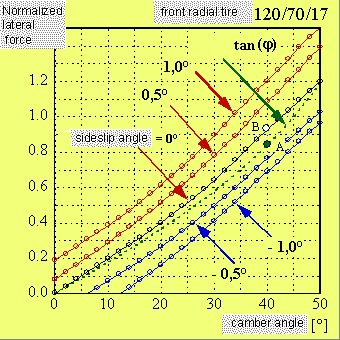
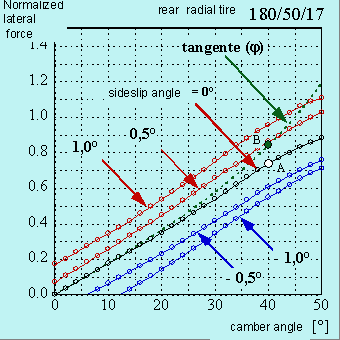
Figure 8. Example of front and rear lateral forces versus roll angle. The dotted lines represented the lateral force required for the equilibrium in the curve.

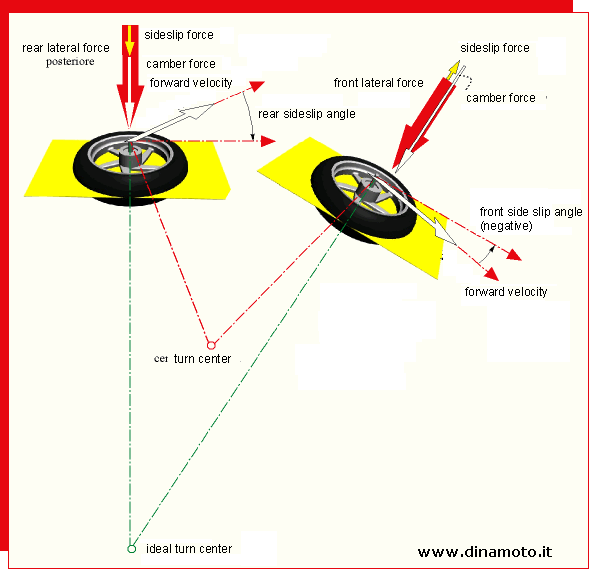
Figure 9.Top view of a motorcycle in the curve.