 |
|
Esempi
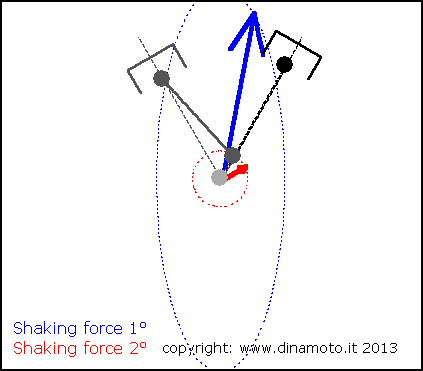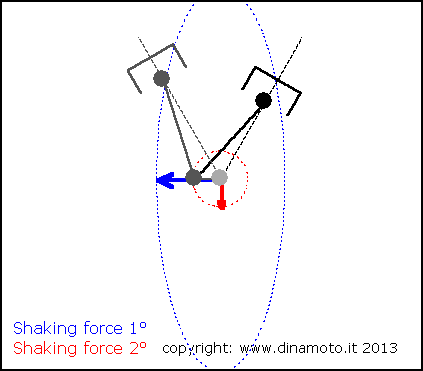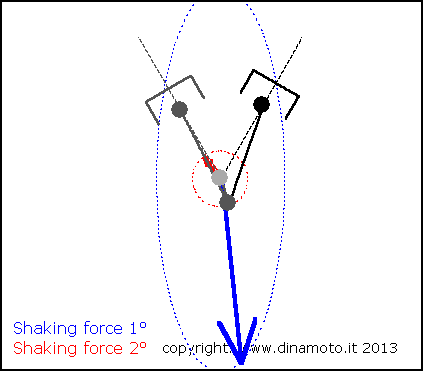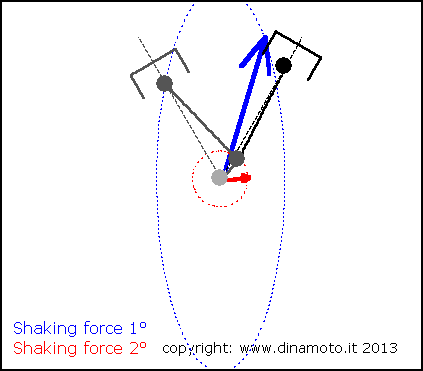
Nelle figure seguenti, la freccia blu indica la forza alterna del 1° ordine, quella rossa la forza alterna del 2° ordine
 |
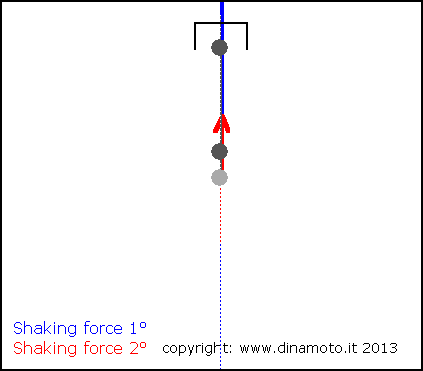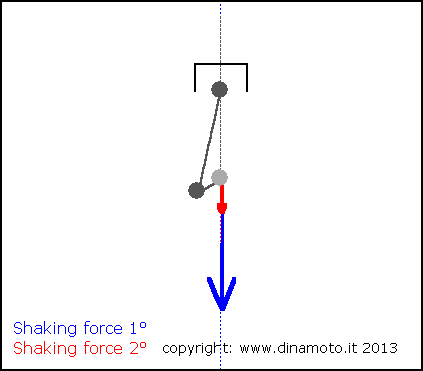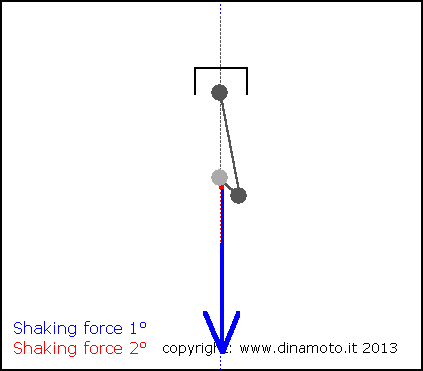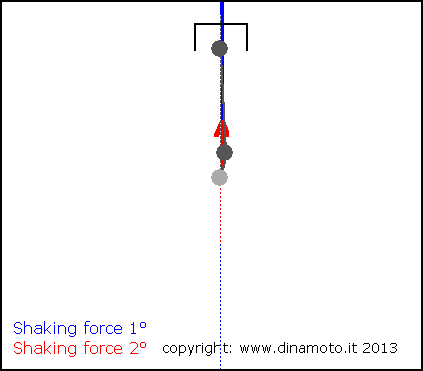 |
|
( Norton Comando) |
|
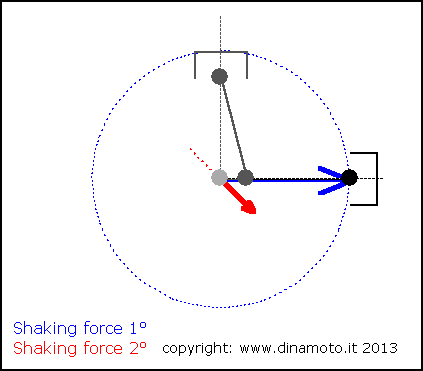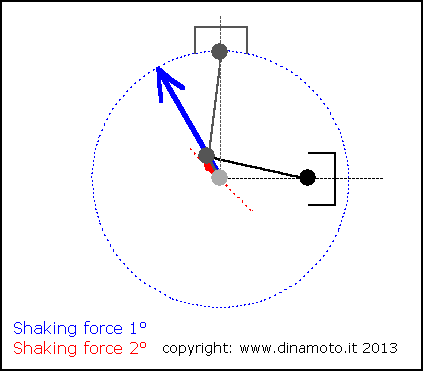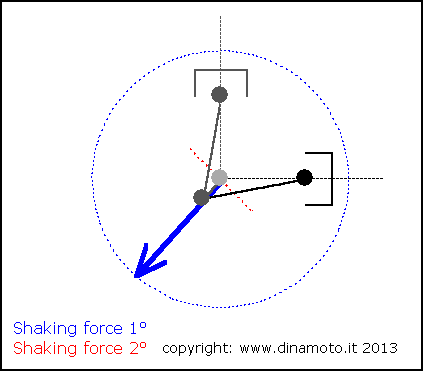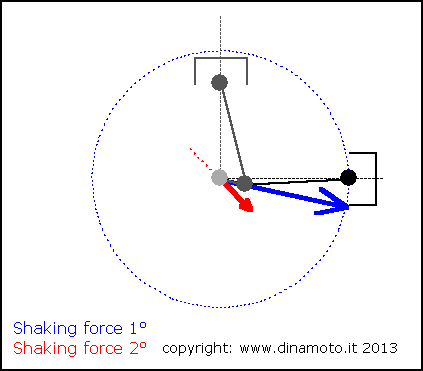 |
 |
|
(Moto Guzzi, Ducati) |
(Harley-Davidson) |
 |
 |
|
( Aprilia 1000 RSV, questo motore ha due alberi di bilanciatura per bilanciare la forza alterna del 1° ordine e il momento) |
( Honda Transalp) |
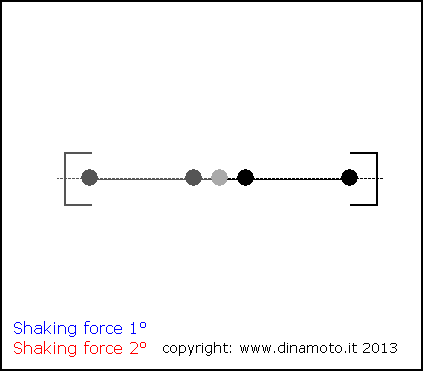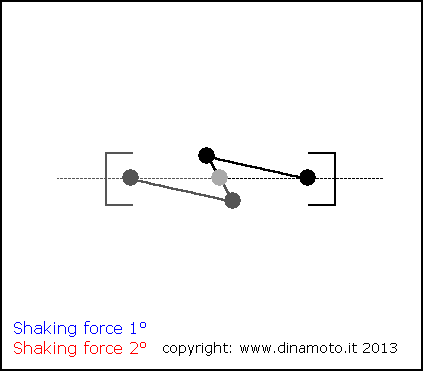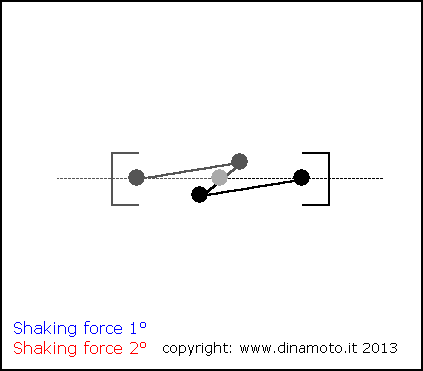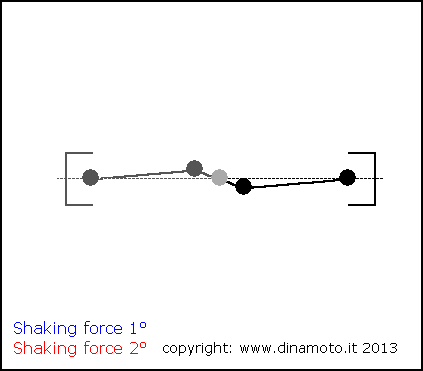 |
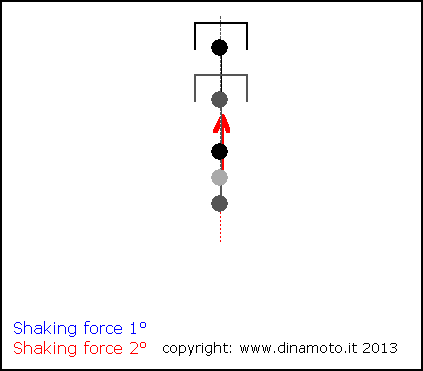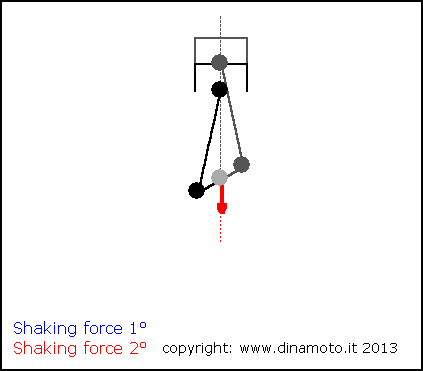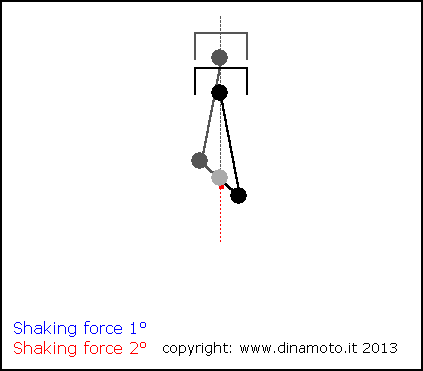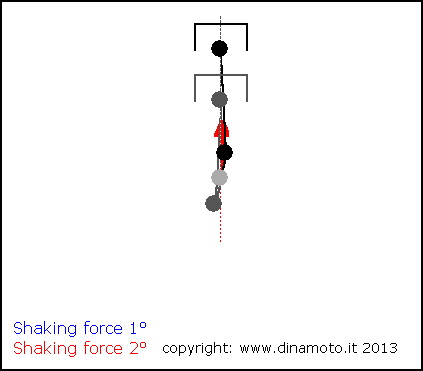 |
|
( BMW boxer) |
( Yamaha TDM 850) |
Ora un pò di teoria
Consideriamo lo schema di un motore a due cilindri rappresentato nella figura seguente

Fig. 1 Schema del motore bicilindrico e delle forze alterne
Le forze sono espresse da:

dove:
mC = massa alternativa situata al piede di biella, composto dalla massa del pistone e la porzione della massa della biella che si considera concentrata presso lo spinotto (circa un terzo);
w = velocità angolare;
r = raggio della manovella;
b = Lunghezza biella;
I b= momento di inerzia della biella residuo(trascurabile);
Le componenti della forza di inerzia primaria (primo ordine) sono:
Va notato che le forze Fn sono estremamente ridotte se confrontate con le forze di inerzia primaria e secondaria.
Le forze di inerzia ruotano nella stessa descrivendo nel piano xy una circonferenza o una ellisse, in funzione delle ampiezze e delle fasi delle due componenti.
L'equilibratura completa è possibile solo se le due componenti hanno le stesse ampiezze e un angolo di fase pari a 90 °. Per raggiungere questa condizione, l'angolo tra le due manovelle deve rispettare questa equazione:
In questo caso, la semplice aggiunta di una massa in opposizione alla forza inerziale primaria è sufficiente ad ottenere un equilibrio completo. Se il diagramma polare della forza primaria è una curva ellittica, l'equilibrio è solo parziale.
Le componenti della forza di inerzia del 2° ordine sono le seguenti:
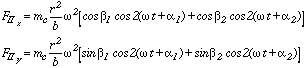
Queste componenti rappresentano una forza, generalmente con una ampiezza non costante, rotante con velocità doppia rispetto a quella della manovella.
Le forze primarie e secondarie dei due cilindri non sono sullo stesso piano. Per questo motivo le coppie sbilanciati tendono a ruotare il motore attorno ad un asse perpendicolare all'asse z. I valori di queste coppie possono essere determinati moltiplicando la forza per la distanza tra i due cilindri.
